
In the field of structural engineering, the second moment of area of the cross-section of a beam is an important property used in the calculation of the beam's deflection and the calculation of stress caused by a moment applied to the beam. Area Moment of Inertia - Typical Cross Sections I Typical cross sections and their Area Moment of Inertia. Related Documents Angle Calculator - Carpenter's Square Calculate angles with a straight board across carpenter's square. Its unit of dimension when working with the International System of Units is meters to the fourth power, m4. Deflection and stress, moment of inertia, section modulus and technical information of beams and columns. In both cases, it is calculated with a multiple integral over the object in question. Corporate Author: NAVAL SURFACE WEAPONS CENTER. for all the point masses that make up the object. The second moment of area is typically denoted with either anįor an axis that lies in the plane or with aįor an axis perpendicular to the plane. Calculation of Moment of Inertia and Shear Area of a Ship Cross-Section. We defined the moment of inertia I of an object to be. It can be calculated using the formula IXY xy dA. Generally, it can't be known which equation is relevant beforehand.The 2nd moment of area, also known as moment of inertia of plane area, area moment of inertia, or second area moment, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. When mass is distributed symmetrically, the POI will be zero.

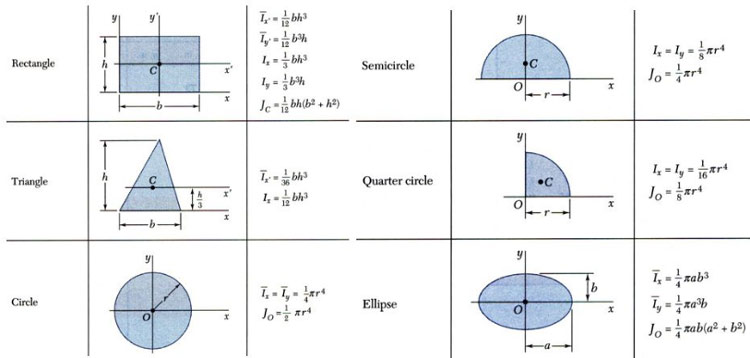
The first equation is valid when the plastic neutral axis cuts through the two flanges, while the second one when it cuts through the web. X_c = \frac is the distance of the plastic neutral axis from the external edge of the web (left edge in figure). The distance of the centroid from the left edge of the section x_c, can be found using the first moments of area, of the web and the two flanges: However, it is crucial that b and h are assigned correct values. Adapting the basic formula for the polar moment of inertia (10.1.5) to our labels, and noting that limits of integration are from 0 to r, we get. We have a comprehensive article explaining the approach to solving the moment of inertia. Solution: The moment of inertia of a rectangular shape such as this one is easily calculated by using the equation I 1/12 bh3. The differential area of a circular ring is the circumference of a circle of radius times the thickness d. The moment of inertia can be derived as getting the moment of inertia of the parts and applying the transfer formula: I I 0 + Ad 2. Determine: The Moments of Inertia, Ixx and Iyy of this section.
The area A and the perimeter P of a channel cross-section, can be found with the next formulas: Moment of Inertia Given: the cross-section. In this page, the two flanges are assumed identical, resulting in a symmetrical U shape. Specifically, the U section is defined by its two flanges and the web. The following figure illustrates the basic dimensions of a U section, as well as, the widely established naming for its components. However, U shaped cross sections can be formed with other materials too (e.g. MOMENT OF INERTIA (I) I, for rectangular and circular sections about their NA can be found using following formulae: I for I-sections, Box sections and channel sections can be found using following formulae: Transfer of axis for Moment of Inertia This formula is used to find MI of a T or other sections, whose NA or CG is not located at the.
The U section (also called channel) is a pretty common section shape, typically used in steel construction. The moment of inertia of a body with the shape of the cross-section is the second moment of this area about the -axis perpendicular to the cross-section, weighted by its density.


 0 kommentar(er)
0 kommentar(er)
